3-A. Machine Learning Models

Machine learning (ML) is a subfield of artificial intelligence (AI) focused on developing algorithms and statistical models that enable computers to learn from and make decisions based on data. Unlike traditional programming, where explicit instructions are given, machine learning systems identify patterns and insights from large datasets, improving their performance over time through experience.

ML encompasses various techniques, including supervised learning, where models are trained on labeled data to predict outcomes; unsupervised learning, which involves discovering hidden patterns or groupings within unlabeled data; and reinforcement learning, where models learn optimal actions through trial and error in dynamic environments. These methods are applied across diverse domains, from natural language processing and computer vision to recommendation systems and autonomous vehicles, revolutionizing how technology interacts with the world.

3.1 Decision Tree and Random Forest

3.1.1 Decision Trees

Decision Trees are intuitive and powerful models used in machine learning to make predictions and decisions. Think of it like playing a game of 20 questions, where each question helps you narrow down the possibilities. Decision trees function similarly; they break down a complex decision into a series of simpler questions based on the data.

Each question, referred to as a “decision,” relies on a specific characteristic or feature of the data. For instance, if you’re trying to determine whether a fruit is an apple or an orange, the initial question might be, “Is the fruit’s color red or orange?” Depending on the answer, you might follow up with another question—such as, “Is the fruit’s size small or large?” This questioning process continues until you narrow it down to a final answer (e.g., the fruit is either an apple or an orange).

In a decision tree, these questions are represented as nodes, and the possible answers lead to different branches. The final outcomes are represented at the end of each branch, known as leaf nodes. One of the key advantages of decision trees is their clarity and ease of understanding—much like a flowchart. However, they can also be prone to overfitting, especially when dealing with complex datasets that have many features. Overfitting occurs when a model performs exceptionally well on training data but fails to generalize to new or unseen data.

In summary, decision trees offer an intuitive approach to making predictions and decisions, but caution is required to prevent them from becoming overly complicated and tailored too closely to the training data.

3.1.2 Random Forest

Random Forests address the limitations of decision trees by utilizing an ensemble of multiple trees instead of relying on a single one. Imagine you’re gathering opinions about a game outcome from a group of people; rather than trusting just one person’s guess, you ask everyone and then take the most common answer. This is the essence of how a Random Forest operates.

In a Random Forest, numerous decision trees are constructed, each making its own predictions. However, a key difference is that each tree is built using a different subset of the data and considers different features of the data. This technique, known as bagging (Bootstrap Aggregating), allows each tree to provide a unique perspective, which collectively leads to a more reliable prediction.

When making a final prediction, the Random Forest aggregates the predictions from all the trees. For classification tasks, it employs majority voting to determine the final class label, while for regression tasks, it averages the results.

Random Forests typically outperform individual decision trees because they are less likely to overfit the data. By combining multiple trees, they achieve a balance between model complexity and predictive performance on unseen data.

Real-Life Analogy

Consider Andrew, who wants to decide on a destination for his year-long vacation. He starts by asking his close friends for suggestions. The first friend asks Andrew about his past travel preferences, using his answers to recommend a destination. This is akin to a decision tree approach—one friend following a rule-based decision process.

Next, Andrew consults more friends, each of whom poses different questions to gather recommendations. Finally, Andrew chooses the places suggested most frequently by his friends, mirroring the Random Forest algorithm’s method of aggregating multiple decision trees’ outputs.

3.1.3 Implementing Random Forest on the BBBP Dataset

This guide demonstrates how to implement a Random Forest algorithm in Python using the BBBP (Blood–Brain Barrier Permeability) dataset. The BBBP dataset is used in cheminformatics to predict whether a compound can cross the blood-brain barrier based on its chemical structure.

The dataset contains SMILES (Simplified Molecular Input Line Entry System) strings representing chemical compounds, and a target column that indicates whether the compound is permeable to the blood-brain barrier or not.

The goal is to predict whether a given chemical compound will cross the blood-brain barrier, based on its molecular structure. This guide walks you through downloading the dataset, processing it, and training a Random Forest model.

Step 1: Install RDKit (Required for SMILES to Fingerprint Conversion)

We need to use the RDKit library, which is essential for converting SMILES strings into molecular fingerprints, a numerical representation of the molecule.

# Install the RDKit package via conda-forge
!pip install -q condacolab
import condacolab
condacolab.install()

# Now install RDKit
!mamba install -c conda-forge rdkit -y

# Import RDKit and check if it's installed successfully
from rdkit import Chem
print("RDKit is successfully installed!")

Step 2: Download the BBBP Dataset from Kaggle

The BBBP dataset is hosted on Kaggle, a popular platform for datasets and machine learning competitions. To access the dataset, you need a Kaggle account and an API key for authentication. Here’s how you can set it up:

Step 2.1: Create a Kaggle Account

1. Visit Kaggle and create an account if you don’t already have one.
2. Once you’re logged in, go to your profile by clicking on your profile picture in the top right corner, and select My Account.

Step 2.2: Set Up the Kaggle API Key

1. Scroll down to the section labeled API on your account page.
2. Click on the button “Create New API Token”. This will download a file named kaggle.json to your computer.
3. Keep this file safe! It contains your API key, which you’ll use to authenticate when downloading datasets.

Step 2.3: Upload the Kaggle API Key

Once you have the kaggle.json file, you need to upload it to your Python environment:

1. If you’re using a notebook environment like Google Colab, use the code below to upload the file:

# Upload the kaggle.json file from google.colab import 
files uploaded = files.upload() 
# Move the file to the right directory for authentication 
!mkdir -p ~/.kaggle !mv kaggle.json ~/.kaggle/ !chmod 600 ~/.kaggle/kaggle.json

1. If you’re using a local Jupyter Notebook: Place the kaggle.json file in a folder named .kaggle within your home directory:
   • On Windows: Place it in C:\Users<YourUsername>.kaggle.
   • On Mac/Linux: Place it in ~/.kaggle.

Step 2.4: Install the Required Libraries

To interact with Kaggle and download the dataset, you need the Kaggle API client. Install it with the following command:

!pip install kaggle

Step 2.5: Download the BBBP Dataset

Now that the API key is set up, you can download the dataset using the Kaggle API:

# Download the BBBP dataset using the Kaggle API 
!kaggle datasets download -d priyanagda/bbbp-smiles 
# Unzip the downloaded file 
!unzip bbbp-smiles.zip -d bbbp_dataset

This code will:

1. Download the dataset into your environment.
2. Extract the dataset files into a folder named bbbp_dataset.

Step 2.6: Verify the Download

After downloading, check the dataset files to confirm that everything is in place:

# List the files in the dataset folder 
import os 
dataset_path = "bbbp_dataset" 
files = os.listdir(dataset_path) 
print("Files in the dataset:", files)

By following these steps, you will have successfully downloaded and extracted the BBBP dataset, ready for further analysis and processing.

Step 3: Load the BBBP Dataset

After downloading the dataset, we’ll load the BBBP dataset into a pandas DataFrame. The dataset contains the SMILES strings and the target variable (p_np), which indicates whether the compound can cross the blood-brain barrier (binary classification: 1 for permeable, 0 for non-permeable).

import pandas as pd

# Load the BBBP dataset (adjust the filename if it's different)
data = pd.read_csv("bbbp.csv")  # Assuming the dataset is named bbbp.csv
print("Dataset Head:", data.head())

Step 4: Convert SMILES to Molecular Fingerprints

To use the SMILES strings for modeling, we need to convert them into molecular fingerprints. This process turns the chemical structures into a numerical format that can be fed into machine learning models. We’ll use RDKit to generate these fingerprints using the Morgan Fingerprint method.

from rdkit import Chem
from rdkit.Chem import AllChem
import numpy as np

# Function to convert SMILES to molecular fingerprints
def featurize_molecule(smiles):
    mol = Chem.MolFromSmiles(smiles)
    if mol:
        return AllChem.GetMorganFingerprintAsBitVect(mol, 2, nBits=1024)
    else:
        return None

# Apply featurization to the dataset
features = [featurize_molecule(smi) for smi in data['smiles']]  # Replace 'smiles' with the actual column name if different
features = [list(fp) if fp is not None else np.zeros(1024) for fp in features]  # Handle missing data by filling with zeros
X = np.array(features)
y = data['p_np']  # Target column (1 for permeable, 0 for non-permeable)

The diagram below provides a visual representation of what this code does:

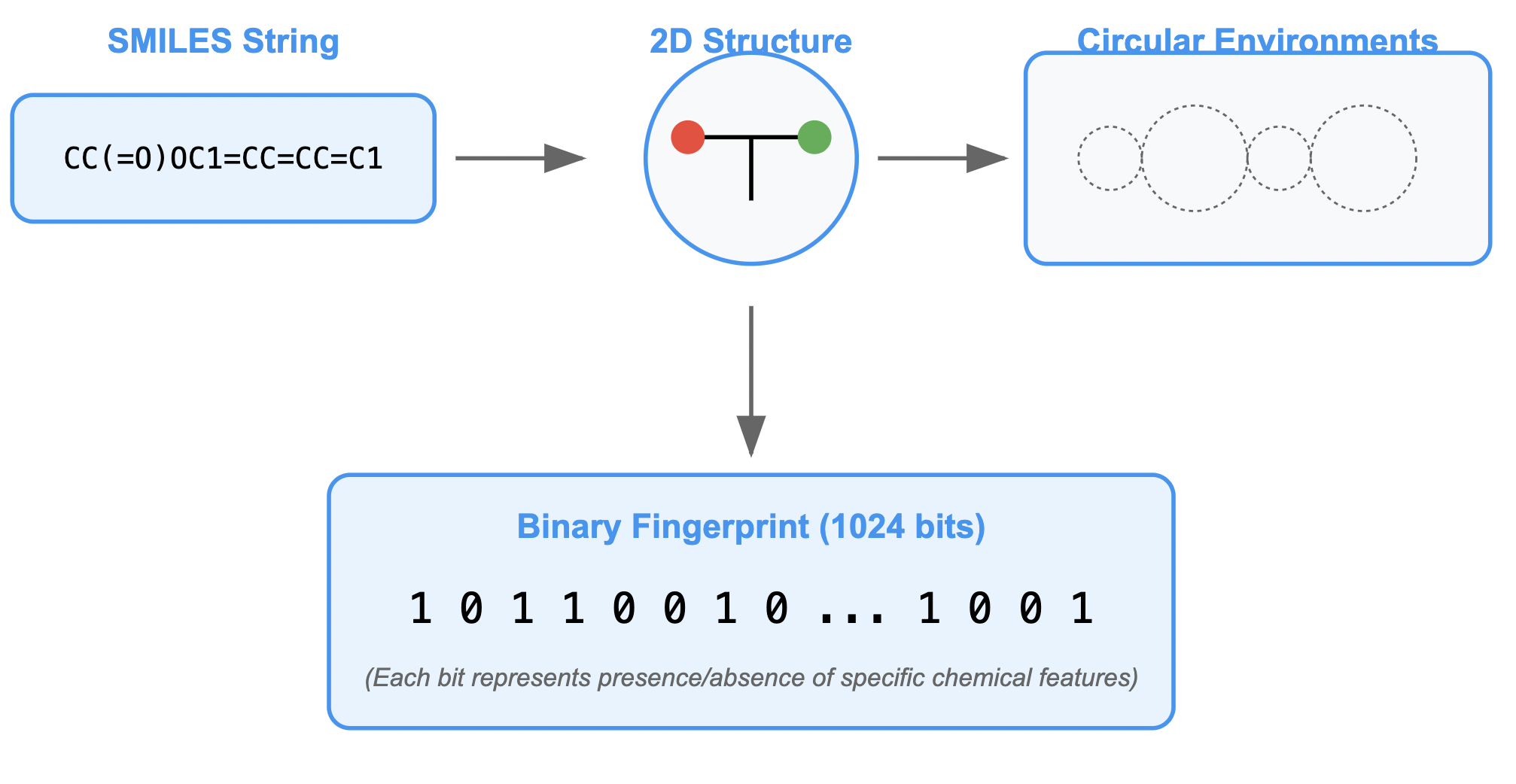
Figure: SMILES to Molecular Fingerprints Conversion Process

Step 5: Split Data into Training and Testing Sets

To evaluate the model, we need to split the data into training and testing sets. The train_test_split function from scikit-learn will handle this. We’ll use 80% of the data for training and 20% for testing.

from sklearn.model_selection import train_test_split

# Split data into train and test sets (80% training, 20% testing)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

The diagram below provides a visual representation of what this code does:

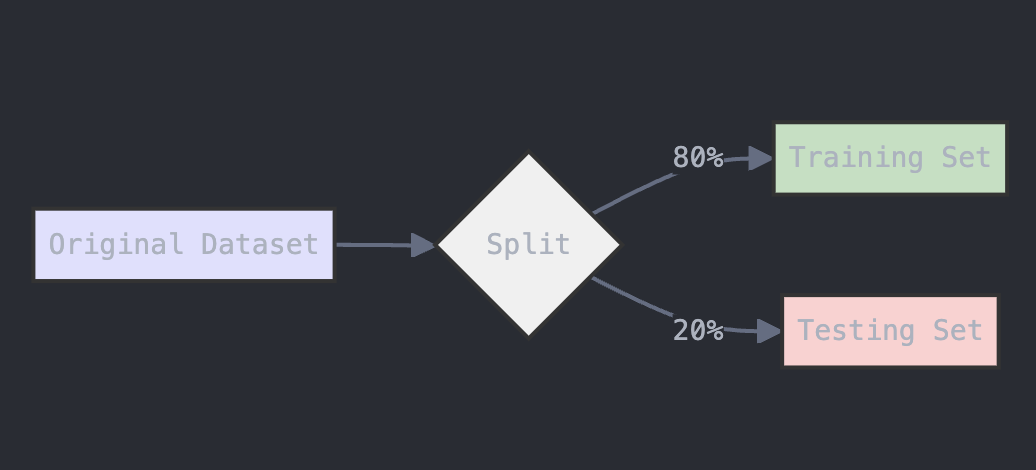
Figure: Data Splitting Process for Training and Testing

Step 6: Train the Random Forest Model

We’ll use the RandomForestClassifier from scikit-learn to build the model. A Random Forest is an ensemble method that uses multiple decision trees to make predictions. The more trees (n_estimators) we use, the more robust the model will be, but the longer the model will take to run. For the most part, n_estimators is set to 100 in most versions of scikit-learn. However, for more complex datasets, higher values like 500 or 1000 may improve performance.

from sklearn.ensemble import RandomForestClassifier

# Train a Random Forest classifier
rf_model = RandomForestClassifier(n_estimators=100, random_state=42)
rf_model.fit(X_train, y_train)

The diagram below provides a visual explanation of what is going on here:

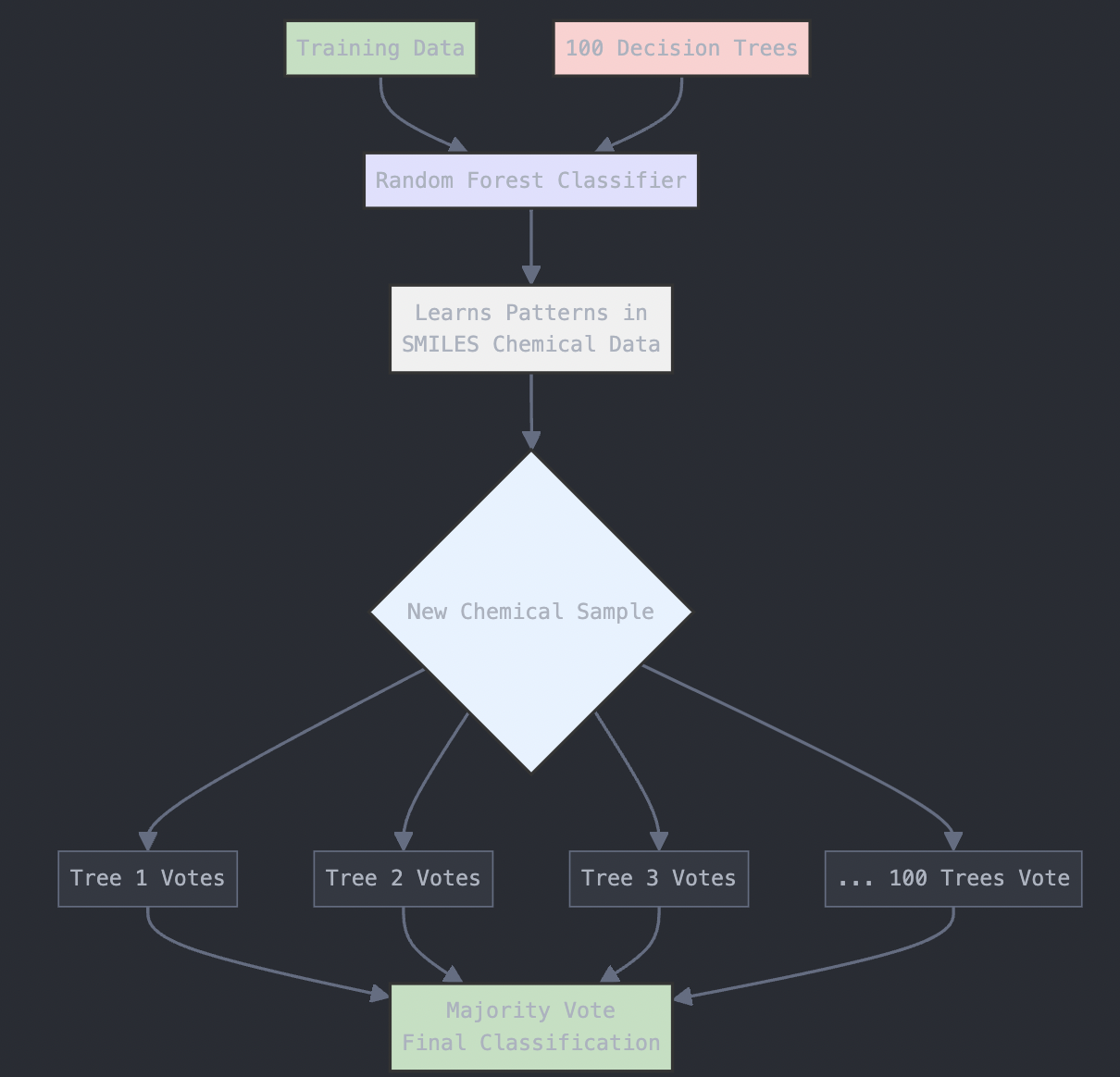
Figure: Random Forest Algorithm Structure

Step 7: Evaluate the Model

After training the model, we’ll use the test data to evaluate its performance. We will print the accuracy and the classification report to assess the model’s precision, recall, and F1 score.

from sklearn.metrics import accuracy_score, classification_report

# Predictions on the test set
y_pred = rf_model.predict(X_test)

# Evaluate accuracy and performance
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)
print("Classification Report:", classification_report(y_test, y_pred))

Model Performance and Parameters

• Accuracy: The proportion of correctly predicted instances out of all instances.
• Classification Report: Provides additional metrics like precision, recall, and F1 score.

In this case, we achieved an accuracy score of ~87%.

Key Hyperparameters:

• n_estimators: The number of trees in the Random Forest. More trees generally lead to better performance but also require more computational resources.
• test_size: The proportion of data used for testing. A larger test size gives a more reliable evaluation but reduces the amount of data used for training.
• random_state: Ensures reproducibility by initializing the random number generator to a fixed seed.

Conclusion

This guide demonstrated how to implement a Random Forest model to predict the Blood–Brain Barrier Permeability (BBBP) using the BBBP dataset. By converting SMILES strings to molecular fingerprints and using a Random Forest classifier, we were able to achieve an accuracy score of around 87%.

Adjusting parameters like the number of trees (n_estimators) or the split ratio (test_size) can help improve the model’s performance. Feel free to experiment with these parameters and explore other machine learning models for this task!

3.1.4 Approaching Random Forest Problems

When tackling a classification or regression problem using the Random Forest algorithm, a systematic approach can enhance your chances of success. Here’s a step-by-step guide to effectively solve any Random Forest problem:

1. Understand the Problem Domain: Begin by thoroughly understanding the problem you are addressing. Identify the nature of the data and the specific goal—whether it’s classification (e.g., predicting categories) or regression (e.g., predicting continuous values). Familiarize yourself with the dataset, including the features (independent variables) and the target variable (dependent variable).

2. Data Collection and Preprocessing: Gather the relevant dataset and perform necessary preprocessing steps. This may include handling missing values, encoding categorical variables, normalizing or standardizing numerical features, and removing any outliers. Proper data cleaning ensures that the model learns from quality data.

3. Exploratory Data Analysis (EDA): Conduct an exploratory data analysis to understand the underlying patterns, distributions, and relationships within the data. Visualizations, such as scatter plots, histograms, and correlation matrices, can provide insights that inform feature selection and model tuning.

4. Feature Selection and Engineering: Identify the most relevant features for the model. This can be achieved through domain knowledge, statistical tests, or feature importance metrics from preliminary models. Consider creating new features through feature engineering to enhance model performance.

5. Model Training and Parameter Tuning: Split the dataset into training and testing sets, typically using an 80-20 or 70-30 ratio. Train the Random Forest model using the training data, adjusting parameters such as the number of trees (n_estimators), the maximum depth of the trees (max_depth), and the minimum number of samples required to split an internal node (min_samples_split). Utilize techniques like grid search or random search to find the optimal hyperparameters.

6. Model Evaluation: Once trained, evaluate the model’s performance on the test set using appropriate metrics. For classification problems, metrics such as accuracy, precision, recall, F1 score, and ROC-AUC are valuable. For regression tasks, consider metrics like mean absolute error (MAE), mean squared error (MSE), and R-squared.

7. Interpretation and Insights: Analyze the model’s predictions and feature importance to derive actionable insights. Understanding which features contribute most to the model can guide decision-making and further improvements in the model or data collection.

8. Iterate and Improve: Based on the evaluation results, revisit the previous steps to refine your model. This may involve further feature engineering, collecting more data, or experimenting with different algorithms alongside Random Forest to compare performance.

9. Deployment: Once satisfied with the model’s performance, prepare it for deployment. Ensure the model can process incoming data and make predictions in a real-world setting, and consider implementing monitoring tools to track its performance over time.

By following this structured approach, practitioners can effectively leverage the Random Forest algorithm to solve a wide variety of problems, ensuring thorough analysis, accurate predictions, and actionable insights.

3.1.5 Strengths and Weaknesses of Random Forest

Strengths:

• Robustness: Random Forests are less prone to overfitting compared to individual decision trees, making them more reliable for new data.

• Versatility: They can handle both classification and regression tasks effectively.

• Feature Importance: Random Forests provide insights into the significance of each feature in making predictions.

Weaknesses:

• Complexity: The model can become complex, making it less interpretable than single decision trees.

• Resource Intensive: Training a large number of trees can require significant computational resources and time.

• Slower Predictions: While individual trees are quick to predict, aggregating predictions from multiple trees can slow down the prediction process.

Section 3.1 – Quiz Questions

1) Factual Questions

Question 1

What is the primary reason a Decision Tree might perform very well on training data but poorly on new, unseen data?

A. Underfitting
B. Data leakage
C. Overfitting
D. Regularization

Question 2

In a Decision Tree, what do the internal nodes represent?

A. Possible outcomes
B. Splitting based on a feature
C. Aggregation of multiple trees
D. Random subsets of data

Question 3

Which of the following best explains the Random Forest algorithm?

A. A single complex decision tree trained on all the data
B. Many decision trees trained on identical data to improve depth
C. Many decision trees trained on random subsets of the data and features
D. A clustering algorithm that separates data into groups

Question 4

When training a Random Forest for a classification task, how is the final prediction made?

A. By taking the median of the outputs
B. By taking the average of probability outputs
C. By majority vote among trees’ predictions
D. By selecting the tree with the best accuracy

2) Conceptual Questions

Question 5

You are given a dataset containing information about chemical compounds, with many categorical features (such as “molecular class” or “bond type”).
Would using a Random Forest model be appropriate for this dataset?

A. No, Random Forests cannot handle categorical data.
B. Yes, Random Forests can naturally handle datasets with categorical variables after encoding.
C. No, Random Forests only work on images.
D. Yes, but only if the dataset has no missing values.

Question 6

Suppose you have your molecule fingerprints stored in variables X and your labels (0 or 1 for BBBP) stored in y.
Which of the following correctly splits the data into 80% training and 20% testing sets?

A.

X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.2, random_state=42)

B.

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

C.

X_train, X_test = train_test_split(X, y, test_size=0.8, random_state=42)

D.

X_train, y_train, X_test, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)